私はJarrett Yeです。論文「間隔反復スケジューリングを最適化するための確率的最短経路アルゴリズム」および「記憶の動態を捉えて間隔反復スケジュールを最適化する」の主著者です。現在、MaiMemo Inc.で働いており、MaiMemoの語学学習アプリ内の間隔反復アルゴリズムの開発を主に担当しています。これらの論文の発表に至るまでの私の学術的な旅の詳細については、「学部生としてACMKDDに論文を発表するまでの道のり」をご参照ください。
このチュートリアル「間隔反復アルゴリズム:初心者から専門家への3日間の旅」は、もともとMaiMemoでの内部プレゼンテーションのために準備したレポートを基にしています。この記事の目的は、間隔反復アルゴリズムがどのように機能するかを詳しく説明し、新しい研究者がこの分野に貢献し、学習技術の進歩を促進することを目指しています。それでは、さっそくこの知的な旅に出発しましょう!
序文
学生時代から、ほとんどの学生は次の2つの事実を直感的に知っています:
- 情報を複数回復習することで、よりよく覚えられる。
- 記憶の消失速度は異なり、すべてを一度に忘れるわけではない。
これらの洞察はさらに次のような疑問を引き起こします:
- 既にどれだけの知識を忘れてしまったかを推定できるか?
- それをどれくらいの速さで忘れているのか?
- 忘却を最小限に抑えるための最適な復習スケジュールは何か?
過去には、これらの質問に答えようとした人はほとんどいませんでした。間隔反復アルゴリズムを開発するには、これらの答えを見つける必要があります。
次の3日間で、間隔反復アルゴリズムを3つの視点から掘り下げていきます:
- 経験的アルゴリズム
- 理論モデル
- 最新の進展
1日目: 経験的アルゴリズムの探求
今日は、最もシンプルでありながら影響力のある経験的アルゴリズムに飛び込むことから旅を始めます。それらの詳細とそれを導くアイデアを明らかにします。しかしまず、「間隔反復」という用語のルーツをたどってみましょう。
間隔反復
間隔反復のテーマに初めて触れる読者のために、「忘却曲線」の概念について学びましょう。
本やその他の手段で何かを学んだ後、私たちはそれを忘れ始めます。これは徐々に起こります。
忘却曲線は、私たちの記憶が知識を保持する方法を示しています。それは独特の軌跡を描きます:積極的な復習がない場合、記憶の減衰は最初は急速であり、時間が経つにつれて遅くなります。
この自然な忘却の傾向に対抗するにはどうすればよいでしょうか?復習の効果を考えてみましょう。
定期的に資料を復習することで、忘却曲線が平坦になります。言い換えれば、情報を忘れる速度が減少します。
ここで疑問が生じます:効率的な記憶保持のためにこれらの復習間隔をどのように最適化できるでしょうか?
各復習の後、特定の保持レベルに対応する間隔が増加することに気づきましたか?短い間隔は馴染みのない内容に適しており、長い間隔はより馴染みのある資料に使用されるべきです。この方法は「間隔反復」として知られ、長期記憶の形成を促進します。
しかし、それはどれほど効果的でしょうか?ここに、間隔反復の利点を示すいくつかの研究があります(出典)。
- Rea & Modigliani 1985, 「拡張練習と集中練習が掛け算の事実とスペリングリストの保持に与える影響」:
トレーニング直後のテストでは、分散練習グループ(70%正解)が集中練習グループ(53%正解)よりも優れた成績を示しました。これらの結果は、間隔効果が学齢期の子供たちや学校で通常教えられるいくつかの種類の教材に適用されることを示しているようです。
- Donovan & Radosevich 1999, 「練習効果の分布に関するメタ分析レビュー:今見える、今見えない」:
全体の平均加重効果サイズは0.46であり、95%信頼区間は0.42から0.50まで広がっていました。...この効果サイズの95%信頼区間にはゼロが含まれていないため、間隔練習が集中練習よりもタスクパフォーマンスの点で有意に優れていたことを示しています。
簡単に言えば、間隔反復を使用する人の62%から64%が、集中反復を使用する人よりも良い結果を得ることを意味します。この効果は他の研究が報告するほど大きくはありませんが、それでも統計的にも実際的にも有意です。
「間隔反復がそんなに効果的なら、なぜもっと普及していないのか?」と思うかもしれません。
主な障害は、学ばなければならない知識の膨大な量です。各知識には独自の忘却曲線があり、手動での追跡とスケジューリングは不可能です。
ここで間隔反復アルゴリズムの役割が重要になります。記憶状態の追跡を自動化し、効率的な復習スケジュールを見つけることです。
これで、間隔反復について基本的な理解ができたと思います。しかし、最適な間隔の計算や効率的な間隔反復のベストプラクティスなど、まだ疑問が残っているかもしれません。これらの質問は、次の章で回答されます。
レビューセクション
| 質問 | 答え |
|---|---|
| 忘却曲線は記憶のどの側面を捉えていますか? | 知識の保持が時間とともにどのように減少するかを示しています。 |
| 復習がない場合、記憶の保持はどのように低下しますか? | 最初は急速に低下し、その後ゆっくりと低下します。 |
| 成功した復習の後、忘却曲線はどのように変化しますか? | 新しい曲線はより平坦になり、忘却の速度が遅くなることを示します。 |
| 間隔反復は異なる教材にどのように対応しますか? | 馴染みのない教材には短い間隔を使用し、馴染みのある教材には長い間隔を使用します。 |
| 間隔反復におけるアルゴリズムの役割は何ですか? | 記憶状態の追跡と効率的な復習スケジュールの自動化を行います。 |
間隔反復の概念を掘り下げると、次の指針について考えることになるかもしれません:
馴染みのない内容には短い間隔を使用し、馴染みのある内容には長い間隔を使用して、将来の異なるタイミングでレビューを散らします。
これらの「短い」または「長い」間隔を正確に定義するものは何でしょうか?さらに、「馴染みのある」教材と「馴染みのない」教材をどのように区別するのでしょうか?
直感的には、教材に馴染みがあるほど忘れる速度が遅くなるため、馴染みのある教材には長い間隔を使用できることがわかります。しかし、忘れたくないほど、間隔は短くするべきです。間隔が短いほど、レビューの頻度が高くなります。
レビューの頻度と忘却の速度の間には矛盾があるように思えます。一方では、より多くのレビューを行ってより多くを覚えたいと考えます。他方では、馴染みのある教材を頻繁にレビューする必要はありません。この矛盾をどのように解決するのでしょうか?
最初のコンピュータ化された間隔反復アルゴリズムの作成者が、記憶の探求の旅にどのように出発したかを見てみましょう。
SM-0
1985年、若い大学生であるピョートル・ヴォズニアックは、忘却の問題に悩んでいました。

上の画像は彼の語彙ノートの1ページを示しています。このノートには2,794語が79ページにわたって記載されていました。各ページには約40組の英語-ポーランド語の単語がありました。これらのレビューを管理することはヴォズニアックにとって頭痛の種でした。最初は、彼には単語を復習するための体系的な計画がなく、時間があるときに復習するだけでした。しかし、彼は重要なことを行いました:いつ復習したか、どれだけの単語を忘れたかを記録し、進捗を測定できるようにしたのです。
彼は1年分のレビューのデータをまとめ、忘却率が40%から60%の間であることを発見しました。これは彼にとって受け入れがたいものでした。彼は、レビューに圧倒されることなく忘却率を下げるための合理的な学習スケジュールが必要でした。最適なレビュー間隔を見つけるために、彼は記憶実験を開始しました。
ヴォズニアックは、忘却率を5%未満に保ちながら、レビュー間隔をできるだけ長くしたいと考えていました。
以下は彼の実験の詳細です:
教材: 40組の英語-ポーランド語の単語ペアが記載された5ページ。
初回学習: 5ページすべての教材を暗記する。英語の単語を見て、ポーランド語の翻訳を思い出し、答えが正しいかどうかを確認する。答えが正しければ、その単語ペアをこの段階から除外する。答えが間違っていれば、後で再度思い出すようにする。すべての答えが正しくなるまでこれを繰り返す。
初回レビュー: ヴォズニアックの以前のレビュー経験に基づき、初回レビューには1日の間隔を採用した。
続く重要なステージ — A、B、C — では次のことが明らかになった:
ステージA: ヴォズニアックは2日、4日、6日、8日、10日の間隔で5ページのノートをレビューした。結果として得られた忘却率はそれぞれ0%、0%、0%、1%、17%だった。彼は2回目のレビューには7日の間隔が最適であると判断した。
ステージB: 新しい5ページのセットを1日後に初回レビューし、7日後に2回目のレビューを行った。3回目のレビューには6日、8日、11日、13日、16日の間隔を使用し、忘却率はそれぞれ3%、0%、0%、0%、1%だった。ヴォズニアックは3回目のレビューには16日の間隔を選択した。
ステージC: 別の新しい5ページのセットを1日、7日、16日の間隔で初回から3回目のレビューを行った。4回目のレビューには20日、24日、28日、33日、38日の間隔を使用し、忘却率はそれぞれ0%、3%、5%、3%、0%だった。ヴォズニアックは4回目のレビューには35日の間隔を選択した。
彼の実験中、次の最適な間隔は前の間隔の約2倍であることに気づきました。最終的に、彼はSM-0アルゴリズムを紙にまとめました。
- I(1) = 1日
- I(2) = 7日
- I(3) = 16日
- I(4) = 35日
- i > 4の場合: I(i) = I(i-1) * 2
- 最初の4回のレビューで忘れた単語は新しいページに移され、新しい教材と一緒に再度繰り返されました。
ここで、$I(i)$は$i^{th}$レビューに使用される間隔を示します。5回目の繰り返しの間隔は前の間隔の2倍に設定されました。この決定は直感的な仮定に基づいていました。SM-0アルゴリズムを2年間使用することで、ヴォズニアックはこの仮説の妥当性を確認するのに十分なデータを収集しました。
SM-0アルゴリズムの目標は明確でした:記憶の減衰率を最小限に抑えながら、レビュー間隔をできるだけ延ばすこと。その限界も明らかでした。つまり、記憶保持を細かいレベルで追跡することができないことです。
それにもかかわらず、SM-0アルゴリズムの効果は明白でした。1986年に最初のコンピュータを手に入れたヴォズニアックは、モデルをシミュレートし、2つの重要な結論を引き出しました:
- 時間が経つにつれて、知識の総量は減少するのではなく増加する
- 長期的には、知識の習得率は比較的一定のままである
これらの洞察は、アルゴリズムが記憶保持とレビューの頻度の間で妥協を達成できることを証明しました。ヴォズニアックは、間隔反復が学習者を無限のレビューの海に溺れさせる必要はないことに気づきました。この気づきは、彼が間隔反復アルゴリズムの改良を続ける動機となりました。
レビューセクション
| 質問 | 答え |
|---|---|
| ヴォズニアックが最適なレビュー間隔を決定するために考慮した2つの要因は何ですか? | 間隔の長さと記憶保持に関連する記憶減衰率。 |
| ヴォズニアックが実験で新しいレビュー間隔を確立するたびに新しい教材を使用した理由は何ですか? | 以前のレビューの間隔の均一性を確保するため。 |
| SM-0アルゴリズムの主な制限は何ですか? | ノートのページをレビューの単位として使用するため、より細かいレベルでの記憶保持の追跡には不向きであること。 |
SM-2
SM-0アルゴリズムはヴォズニアックの学習に有益であることが証明されましたが、いくつかの問題が彼に改良を求めさせました:
-
最初のレビュー(1日後)で単語を忘れた場合、次のレビュー(7日後および16日後)でも忘れる可能性が高くなります。これは、以前に忘れなかった単語と比較してのことです。
-
忘れた単語で構成された新しいノートページは、レビューのスケジュールが同じであっても忘れる可能性が高くなります。
これらの観察から、すべての教材が同じ難易度ではないことに気づきました。異なる難易度の教材には異なるレビュー間隔が必要です。
その結果、1987年に最初のコンピュータを手に入れた後、ヴォズニアックは2年間の記録とSM-0アルゴリズムから得た洞察を活用して、SM-2アルゴリズムを開発しました。Ankiの内蔵アルゴリズムはSM-2アルゴリズムの変種です。
SM-2の詳細:
- 覚えたい情報を小さな質問と回答のペアに分解します。
- 各質問と回答のペアを次の間隔(日数)でレビューします:
-
$I(1) = 1$
-
$I(2) = 6$
-
$n > 2$の場合、$I(n) = I(n-1) \times EF$
- $EF$—イーズファクター(Ease Factor)、初期値は2.5
- 各レビュー後、$\text{newEF} = EF + (0.1 - (5-q) \times (0.08 + (5-q) \times 0.02))$
- $\text{newEF}$—レビュー後に更新されたイーズファクターの値
- $q$—レビューの品質評価、0から5の範囲。3以上の場合、学習者は覚えており、3未満の場合、学習者は忘れています。
-
学習者が忘れた場合、その質問と回答のペアの間隔は同じEFで$I(1)$にリセットされます。
-
Ankiのアルゴリズムは完全に同じではなく、いくつかの修正が加えられていることは注目に値します。
SM-2アルゴリズムは、質問と回答のペアをどのくらいの頻度でレビューするかにレビューのフィードバックを追加します。EF(Ease Factor)が低いほど、間隔の乗数係数が小さくなります。言い換えれば、間隔の成長が遅くなります。
SM-2アルゴリズムには、今日でも人気のある間隔反復アルゴリズムとなっている3つの主な強みがあります:
-
教材を小さな質問と回答のペアに分解します。これにより、各教材に対して個別のスケジュールを作成することが可能になります。
-
「Ease Factor」と評価を使用します。これにより、アルゴリズムは簡単な教材と難しい教材を区別し、それぞれを異なるスケジュールで管理できます。
-
比較的シンプルで計算コストが低いため、どのデバイスでも簡単に実装できます。
レビューセクション
| 質問 | 答え |
|---|---|
| なぜレビュー中に忘れた教材に対して長い間隔を設定すべきではないのですか? | その教材の忘却速度は遅くならないためです。言い換えれば、忘却曲線は平坦になりません。 |
| ある教材が他の教材よりも覚えにくいことを示すものは何ですか? | 忘れた教材が含まれるページは、再度忘れる可能性が高いことです。 |
| SM-2アルゴリズムに「Ease Factor」と評価を組み込む実際的な目的は何ですか? | これにより、ユーザーのパフォーマンスに基づいて将来のレビュー間隔を調整し、簡単な教材と難しい教材を区別することができます。 |
| 教材を小さな部分に分解することの利点は何ですか? | 各個別の情報に対して適切なスケジュールを見つけることができます。 |
SM-4
SM-4の主な目的は、前身であるSM-2アルゴリズムの適応性を向上させることです。SM-2は、イーズファクターや評価に基づいて個々のフラッシュカードのレビュースケジュールを微調整できますが、これらの調整は全体的な学習プロセスを考慮せずに行われます。
言い換えれば、SM-2は各フラッシュカードを独立したエンティティとして扱います。これを克服するために、SM-4は既存の間隔計算式を置き換える最適間隔(OI)マトリックスを導入します:

最適間隔(OI)マトリックスでは、行が教材の難易度を示し、列がその教材を見た回数を示します。最初は、マトリックスのエントリはカードを再度レビューするまでの期間を決定するSM-2の式を使用して埋められます。
新しいカードが古いカードの調整の恩恵を受けられるように、レビュー中にOIマトリックスは継続的に更新されます。主な考え方は、OIマトリックスがX日待つように指示し、学習者が実際にX+Y日待っても高評価を得られる場合、OI値をXとX+Yの間の何かに変更するというものです。
理由は簡単です:学習者がX+Y日待っても高評価を得られるなら、古いOI値はおそらく短すぎたということです。もっと長くしましょう!
この考え方により、SM-4は他の類似カードからの情報に基づいてカードのスケジュールを調整できる最初のアルゴリズムとなりました。しかし、以下の理由でヴォズニアックが期待したほどにはうまく機能しませんでした:
- 各レビューはマトリックスの1つのエントリしか変更しないため、OIマトリックス全体を改善するには多くの時間がかかります。
- 長いレビュー間隔(数年または数十年)では、対応するマトリックスエントリを埋めるのに十分なデータを収集するのに時間がかかりすぎます。
これらの問題に対処するために、SM-5アルゴリズムが設計されました。しかし、スペースの制限のため、ここでは詳細には触れません。
レビューセクション
| 質問 | 答え |
|---|---|
| SM-2アルゴリズムの適応性が制限されている理由は何ですか? | 各フラッシュカードのスケジュール調整が個別に行われ、アルゴリズムはユーザーの記憶全体を「見る」ことができないためです。 |
| SM-4が適応性を向上させるために導入した要素は何ですか? | 最適間隔マトリックスと動的な間隔調整ルールです。 |
| SM-4における間隔調整の基本原則は何ですか? | 学習者が長い間隔で良い記憶を示す場合、元の間隔を長くし、逆の場合も同様です。 |
まとめ
1885年に初めて発見された忘却曲線は、私たちがどのように記憶し、忘れるかを示しています。1985年に、最初のコンピュータアルゴリズムが間隔反復のために開発され、最適なレビューのスケジュールを見つけることを目指しました。このセクションでは、経験に基づくアルゴリズムの発展の進行を概説しました:
- SM-0は、特定の個人と特定の種類の教材に対して最適なレビュー間隔を決定するための実験データを収集しました(ここで「最適」とは何かをヴォズニアックが定義しました)。
- SM-2は、アルゴリズムをコンピュータアプリケーション向けにデジタル化し、より詳細なカードレベルを導入し、適応的なイーズファクターと評価を組み込みました。
- SM-4は、最適間隔マトリックスと間隔を調整するためのルールを導入し、多様な学習者に対するアルゴリズムの適応性をさらに向上させました。
経験的な観察は、間隔反復を理解するための貴重な視点を提供しますが、理論的な理解がなければそれを改善するのは難しいです。次に、間隔反復の理論的側面に飛び込んでいきます。
2日目: 理論モデルの理解
間隔反復は理論的な分野のように聞こえますが、私は経験的アルゴリズムについて多くの時間を費やして話してきました。なぜでしょうか?
それは、経験的証拠の基盤がなければ、理論的な議論は価値がないからです。人間の記憶の挙動についての直感は正確でないかもしれません。したがって、次に議論する理論も、これまでに学んだことから始めて、現実に基づいていることを確認します。
記憶の2つの要素
ここで考えてみてください:記憶の状態を説明する際にどのような要素を考慮しますか?
ロバート・A・ビョーク以前は、多くの研究者が記憶の強度を使って、人々がどれだけよく何かを覚えているかを話していました。
忘却曲線をもう一度見てみましょう:
まず、**記憶保持(想起確率)**が、記憶の状態を特徴づける重要な変数として浮かび上がります。日常生活では、忘却はしばしば確率的な現象として現れます。今日覚えた単語が10日後に思い出されるか、20日後に忘れられるかを誰も明確に断言することはできません。
想起確率だけで記憶の状態を説明するのに十分でしょうか?上記の忘却曲線に水平線を引くことを想像してみてください。各曲線は同じ想起確率の点で水平線と交差しますが、曲線は異なります。忘却率も記憶状態の説明に確実に考慮されるべきです。
この問題に対処するためには、忘却曲線の数学的特性を掘り下げる必要があります。これは、曲線をプロットするための大量のデータを必要とする作業です。このチュートリアルのデータは、語学学習アプリケーションMaiMemoによって作成されたオープンデータセットから取得されています。
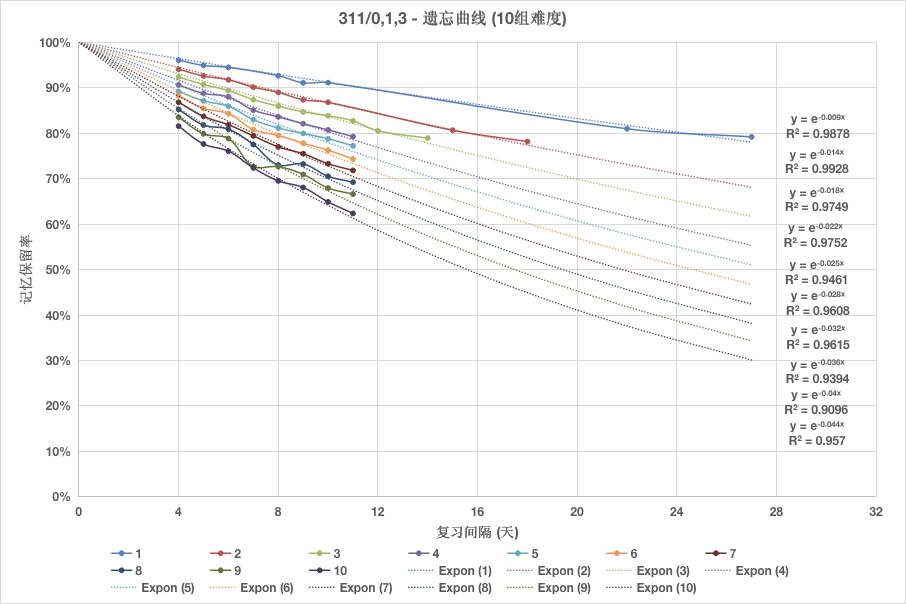
上の図から、忘却曲線は負の指数関数で近似できることがわかります。忘却の速度は、この関数の減衰定数で特徴付けることができます。
忘却曲線のフィッティング式を得るために、次の方程式を書くことができます:
$$ \begin{aligned} R = \exp\left[\frac{t \ln{0.9}}{S}\right] \end{aligned} $$
この方程式では、$R$は想起確率、$S$は記憶の安定性(または記憶の強度)、$t$は最後のレビューから経過した時間を表します。
$S$と忘却曲線の形状の関係は、次の図で見ることができます:
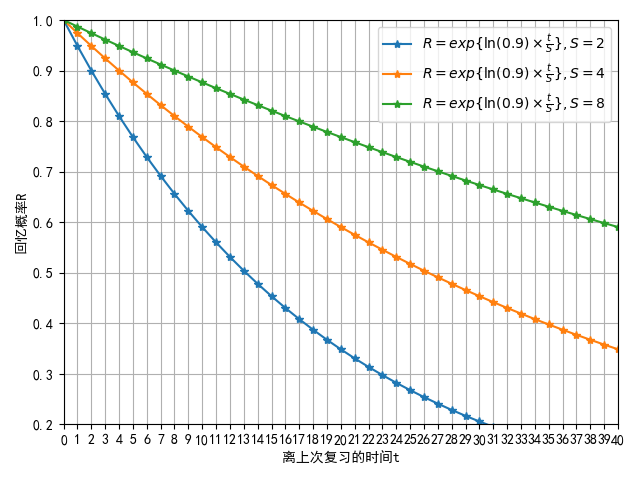
記憶の安定性$S$は、「想起確率」$R$が100%から90%に低下するまでに必要な時間として定義されます。(科学文献では、50%の値がよく使用され、その場合、「記憶の半減期」という用語が使われます。)
ビョークが提案した記憶の2つの要素 — 検索強度と保存強度 — は、ここで定義された想起確率と記憶の安定性に正確に対応します。
この方程式から次の観察が得られます:
-
$t=0$のとき、$R=100%$です。これは、成功した想起の直後には忘却のプロセスがまだ始まっておらず、想起の確率が最大値の100%であることを意味します。
-
$t$が無限大に近づくと、$R$はゼロに近づきます。これは、何かを一度も復習しなければ、最終的にはそれを忘れてしまうことを意味します。
-
負の指数関数の一階導関数は負であり、その絶対値は減少しています(つまり、二階導関数は正です)。これは、忘却が最初は速く、その後徐々に遅くなるという経験的観察と一致します。
このようにして、記憶の2つの要素を定義しましたが、何かが欠けているようです。
レビュー後に忘却曲線の形状が変化すると、記憶の安定性も変化します。この変化は、レビュー時の想起確率と以前の記憶の安定性の値だけに依存するわけではありません。
この主張を裏付ける証拠はあるでしょうか?何かを初めて学ぶときを考えてみてください:記憶の安定性と想起確率はどちらもゼロです。しかし、それを学んだ後は、想起確率は100%になり、記憶の安定性は学んだ教材の特定の特性に依存します。
覚えようとしているもの自体に、記憶に影響を与える特性があります。直感的には、この変数は教材の難易度です。
教材の難易度を考慮に入れると、記憶の3要素モデルが完成します。
レビューセクション
| 質問 | 答え |
|---|---|
| なぜ記憶の強度という単一の変数では記憶の状態を十分に説明できないのですか? | 単一の変数では不十分です。なぜなら、忘却曲線は記憶保持レベルと忘却速度の両方を包含しているからです。 |
| 記憶保持の度合いを測定する変数は何ですか? | 想起確率。 |
| 忘却曲線を近似できる関数は何ですか? | 指数関数。 |
| 忘却の速度を測定する変数は何ですか? | 減衰定数。 |
| 記憶の安定性の定義は何ですか? | 想起確率が100%から所定の割合(通常は90%)に低下するまでに必要な時間。 |
記憶の3要素モデル
用語を詳しく見てみましょう:
- 安定性: 特定の記憶の想起確率が100%から90%に低下するまでに必要な時間。
- 想起可能性(想起確率): 特定の記憶を特定の瞬間に想起する確率。
- 難易度: 特定の記憶に関連する固有の複雑さ。
想起可能性と保持率の違いは、前者が特定の記憶を想起する確率を指すのに対し、後者は記憶の集団に対する平均的な想起確率を指す点です。この用語はすべての研究者に普遍的に採用されているわけではありませんが、この記事ではこの用語を使用します。
任意の記憶の想起可能性を、$n$回の成功した想起後の時間$t$で定義することができます:
$$ R_n(t) = \exp\left[\cfrac{t\ln{0.9}}{S_n}\right] $$
$S_n$がレビュー間の間隔として使用される場合、この方程式は間隔反復アルゴリズムと記憶モデルのギャップを埋めることができます:
$$ R_n(t) = \exp\left[\cfrac{t\ln{0.9}}{I_1\prod\limits_{i=2}^{n}C_i}\right] $$
ここで:
- $I_1$ denotes the initial interval after the first review.
- $C_i$ represents the ratio of the $i$-th interval and the preceding $i-1$-th interval.
間隔反復アルゴリズムの目的は、$I_1$と$C_i$を正確に計算し、異なる学生、教材、およびレビューのスケジュールにわたる記憶の安定性を決定することです。
SM-0およびSM-2アルゴリズムの両方で、$I_1$は1日に等しいです。SM-0では、$C_i$は所定の定数ですが、SM-2では、$C_i$は各レビュー時にカードに与えられた評価に応じて調整される可変のイーズファクター(EF)です。
ここで考えるべき質問は、$C_i$と記憶の3つの要素の関係は何かということです。
以下は、Wozniakの経験的観察結果であり、MaiMemoのような語学学習プラットフォームのデータによって裏付けられています:
- 安定性の影響: 高い$S$は小さい$C_i$をもたらします。これは、記憶がより安定するにつれて、その後の安定化がますます難しくなることを意味します。
- 想起可能性の影響: 低い$R$は大きい$C_i$をもたらします。これは、想起確率が低い状態での成功した想起が、安定性の大きな増加につながることを意味します。
- 難易度の影響: 高い$D$は小さい$C_i$をもたらします。これは、教材の複雑さが高いほど、各レビュー後の安定性の増加が小さくなることを意味します。
複数の要因が関与するため、$C_i$の計算は難しいです。SuperMemoは、$C_i$を多変数関数として表現する多次元マトリックスを使用し、ユーザーの学習過程でマトリックスの値を調整して現実のデータに近づけます。
上記の方程式では、$C_i$は次の間隔の比率を示します。アルゴリズム自体では、$C_i$は安定性の増加を意味します。混乱を避けるために、SuperMemoの用語を採用します:安定性増加(SInc)。これは、レビュー前後の記憶の安定性の_相対的な_増加を表します。
次に、安定性増加について詳しく説明します。
レビューセクション
| 質問 | 答え |
|---|---|
| 記憶の3要素モデルに含まれる変数は何ですか? | 記憶の安定性、記憶の想起可能性、記憶の複雑さ。 |
| 想起可能性と保持率の違いは何ですか? | 前者は個々の記憶に関するものであり、後者は大規模な記憶集団に関するものです。 |
| 記憶の3要素モデルと間隔反復アルゴリズムを結びつける2つの値は何ですか? | 初期間隔$I_1$と連続する間隔の比率$C_i$。 |
| $C_i$は何と呼ばれますか? | 安定性増加。 |
記憶の安定性増加
この章では、記憶の難易度の影響を無視し、記憶の安定性増加(SInc)、安定性(S)、および想起可能性(R)の関係に焦点を当てます。
以下の分析のデータは、SuperMemoユーザーから収集され、Wozniakによって分析されました。
安定性増加のS依存性
安定性増加(SInc)マトリックスを調査したところ、Wozniakは、特定の想起可能性(R)のレベルに対して、安定性(S)に関するSIncの関数が負のべき関数で近似できることを発見しました。

安定性増加(Y軸)と安定性(X軸)の両方の対数を取ると、次の曲線が得られます:

これは、「Sが増加するにつれて、$C_i$は減少する」という以前の定性的な結論を支持しています。
想起可能性に対する安定性増加の依存性
間隔効果が予測するように、想起可能性(R)が低いほど、安定性増加(SInc)は大きくなります。複数のデータセットを分析した結果、Rが減少するにつれてSIncが指数関数的に増加することが観察されました。

想起可能性(X軸)の対数を取ると、次の曲線が得られます:

驚くべきことに、Rが100%のとき、SIncは1を下回ることがあります。分子レベルの研究は、レビュー中に記憶の不安定性が増加することを示唆しています。これにより、教材を頻繁にレビューすることが学習者にとって有益ではないことが再び証明されました。
時間の経過に伴うSIncの値の線形増加

時間(t)が増加するにつれて、想起可能性(R)は指数関数的に減少し、安定性増加(SInc)は指数関数的に増加します。これらの2つの指数は互いに相殺し、ほぼ線形の曲線を生成します。
記憶の安定性増加の予測値
学習の最適化にはいくつかの基準があります。特定の保持率を目標にすることも、記憶の安定性を最大化することもできます。いずれの場合も、予測される安定性の増加を理解することは有益です。
予測される安定性増加を次のように定義します:
$$ E(SInc) = SInc \times R $$
この方程式は興味深い結果をもたらします:予測される安定性増加の最大値は、保持率が30%から40%の間にあるときに発生します。

重要なのは、予測される安定性増加の最大値が必ずしも最速の学習速度を意味するわけではないということです。最も効率的なレビューのスケジュールについては、今後のSSP-MMCアルゴリズムを参照してください。
レビューセクション
| 質問 | 答え |
|---|---|
| 安定性増加と記憶の安定性の関係を説明する数学的関数は何ですか? | 負のべき関数。 |
| 安定性増加と記憶の想起可能性の関係を説明する数学的関数は何ですか? | 指数関数。 |
記憶の複雑さ
記憶の安定性は、ここでは記憶の複雑さと呼ばれる記憶の質にも依存します。効率的なレビューセッションのためには、知識の関連付けがシンプルでなければなりません。たとえ知識自体が複雑であってもです。フラッシュカードは複雑な知識構造をカプセル化できますが、個々のフラッシュカードは原子的であるべきです。
2005年に、Wozniakは複合記憶のレビューを説明する方程式を策定しました。彼は、複合記憶の安定性が回路の抵抗と同様に振る舞うことを観察しました。
*注: 複合という用語は、より単純な要素で構成されていることを強調するために、複雑という用語の代わりに使用されています。

複合知識からは2つの主要な結論が導き出されます:
- 追加の情報断片は干渉を引き起こします。言い換えれば、サブメモリAがサブメモリBを不安定にし、その逆もまた然りです。
- レビュー中に記憶のサブコンポーネントを均等に刺激することは非常に難しいです。
例えば、2つの穴埋めフィールドを記憶する必要がある複合フラッシュカードがあるとします。両方の空欄を覚えるのが同じくらい難しいと仮定します。したがって、複合記憶の想起可能性は、そのサブメモリの想起可能性の積となります:
$$ R = R_a \times R_b $$
これを忘却曲線の方程式に代入すると、次のようになります:
$$ R = e^{ \frac{t \ln 0.9}{S_a}} \times e^{ \frac{t \ln 0.9}{S_b}} = e^{ \frac{t \ln 0.9}{S}} $$
ここで、$S$はこの複合記憶の安定性を示します。次のことが推測できます:
$$ \frac{t \ln 0.9}{S} = \frac{t \ln 0.9}{S_a} + \frac{t \ln 0.9}{S_b} $$
Leading to:
$$ S = \frac{S_a \times S_b}{S_a + S_b} $$
驚くべきことに、複合記憶の安定性は、その構成要素の各記憶の安定性よりも低くなります。また、複合記憶の安定性は、より難しいサブ記憶の安定性に近くなります。
複雑さが増すにつれて、記憶の安定性はゼロに近づきます。これは、全体として本全体を記憶する方法が、継続的に再読すること以外にないことを意味します。これは無駄なプロセスです。
レビューセクション
| 質問 | 答え |
|---|---|
| 複合記憶の想起可能性$R$とその構成要素の想起可能性$R_a, R_b$の関係は何ですか? | $R = R_a \times R_b$。複合記憶の想起可能性は、その構成要素の想起可能性の積です。 |
| 複合記憶の安定性$S$は、その構成要素の安定性$S_a, S_b$よりも大きくなりますか? | 複合記憶の安定性は、その構成要素の安定性よりも低くなります。 |
| 複合記憶の構成要素の数が増えると、複合記憶の安定性はどう変化しますか? | 徐々に減少し、漸近的にゼロに近づきます。 |
3日目: 最新の進展
記憶の理論を学んだ後は、それを実践に移す時です。次のセクションでは、これらの記憶理論をどのように使用して間隔反復アルゴリズムを開発し、ユーザーの学習効率を向上させるかを紹介します。
ここから先はレビューセクションがなくなり、難易度が急激に上がるので、準備をしておいてください!
データ収集
データは間隔反復アルゴリズムの生命線です。適切で包括的かつ正確なデータを収集することが、間隔反復アルゴリズムの能力の限界を決定します。
学習者の記憶状態を正確に推定するためには、記憶の基本的な挙動を定義する必要があります。考えてみましょう:記憶イベントの重要な属性は何でしょうか?
最も基本的な要素は簡単に思い浮かびます:誰(主体)、いつ(時間)、何(記憶)。記憶についてさらに探求すると、何が記憶されたか(内容)、どれだけよく記憶されたか(応答)、どれくらいの時間がかかったか(所要時間)などがあります。応答は、アルゴリズムにいくつかの評価を組み込むことでさらに精緻化できます。
これらの属性を考慮に入れて、タプルを使用して記憶イベントを記録することができます:
$$ e := (\text{user}, \text{item}, \text{time}, \text{response}, \text{time spent}) $$
このイベントは、特定のアイテムに対するユーザーの応答とコストを特定の時間に記録します。例えば:
$$ e := (\text{Jarrett}, \text{apple}, \text{2022-04-01 12:00:01}, \text{Forgotten}, \text{5s}) $$
つまり、ジャレットは2022年4月1日の12:00:01に「apple」という単語を復習し、忘れてしまい、このフラッシュカードの復習に5秒かかりました。
この基本的な記憶イベントの定義を使用して、興味深い情報を抽出および計算することができます。
例えば、間隔反復では、2回の反復間の間隔が非常に重要です。上記の記憶イベントを使用して、ユーザーとアイテムごとにデータをグループ化し、時間でソートし、隣接する2つのイベントの時間を引くことで間隔を取得できます。一般的に、計算ステップを節約するために、間隔はイベントに直接記録することができます。これにより、ストレージの冗長性が発生しますが、計算時間を節約できます。
間隔に加えて、フィードバックの履歴シーケンスも重要です。例えば、「忘れた、覚えた、覚えた、覚えた」や「1日、3日、6日、10日」は、記憶の履歴をより包括的に反映し、記憶イベントに直接記録することができます:
$$ e_{i} := (\text{user}, \text{item}, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}, \Delta t_i, r_i) $$
データに興味がある場合は、MaiMemoからオープンソースデータセットをダウンロードして、自分で分析することができます。
DSRモデル
データが揃ったところで、どう活用するのでしょうか?2日目の記憶の3要素モデルを振り返ると、知りたいのは記憶状態の3つの属性です。しかし、現在のデータセットにはこれが含まれていません。したがって、このセクションの目標は、記憶イベントデータを記憶状態に変換し、それらの関係を明らかにすることです。
記憶状態
DSRモデルの3つの文字は、難易度(Difficulty)、安定性(Stability)、想起可能性(Retrievability)を表しています。想起可能性は、特定の瞬間に記憶を想起する確率を反映しています。確率論的には、記憶イベントは2つの可能な結果しかない単一のランダム実験であり、その成功確率は想起可能性に等しいです。
したがって、想起可能性を測定する最も簡単な方法は、同じ記憶に対して無数の独立した実験を行い、成功した想起の頻度を数えることです。しかし、この方法は実際には実行不可能です。なぜなら、記憶を実験することでその状態が変わってしまうため、観察者として記憶に影響を与えずに測定することはできないからです。 注:現在の神経科学のレベルでは、神経レベルで記憶状態を測定することは不可能であるため、このアプローチも利用できません。
では、他に方法はないのでしょうか?現在、2つの妥協的な測定方法があります:(1)学習教材の違いを無視する:SuperMemoとAnkiはこのアプローチを使用しています。(2)学習者の違いを無視する:MaiMemoはこのアプローチを使用しています。
学習教材の違いを無視するということは、想起可能性を測定する際に、ユーザーが学習している内容を除いて、同じ属性を持つデータを同じユーザーから収集することを意味します。1人の学習者と1つの教材に対して複数の独立した実験を行うことはできませんが、1人の学習者と複数の教材(例えばフラッシュカード)に対しては可能です。一方、学習者の違いを無視するということは、同じ教材を学習している複数の学習者からデータを収集することを意味します。
MaiMemoのデータ量が十分であることを考慮して、このセクションでは学習者の違いを無視する測定方法のみを紹介します。学習者の違いを無視した後、新しいグループの記憶イベントを取得できます:
$$ e_{i} := (item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}, \Delta t_i, p_i, N) $$
ここで、Nは同じ教材を記憶し、同じ反復履歴を持つ学習者の数です。想起可能性$p=\frac{n_{r=1}}{N}$は、これらの学習者の中で成功した想起の割合です。Nが十分に大きい場合、この比率$n_{r=1}/N$は真の想起可能性に近づきます。
想起可能性が計算された後、安定性を簡単に計算できます。収集されたデータに基づいて、指数関数を使用してこのデータを近似し、同じ$(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}})$を持つグループの記憶の安定性を計算できます。
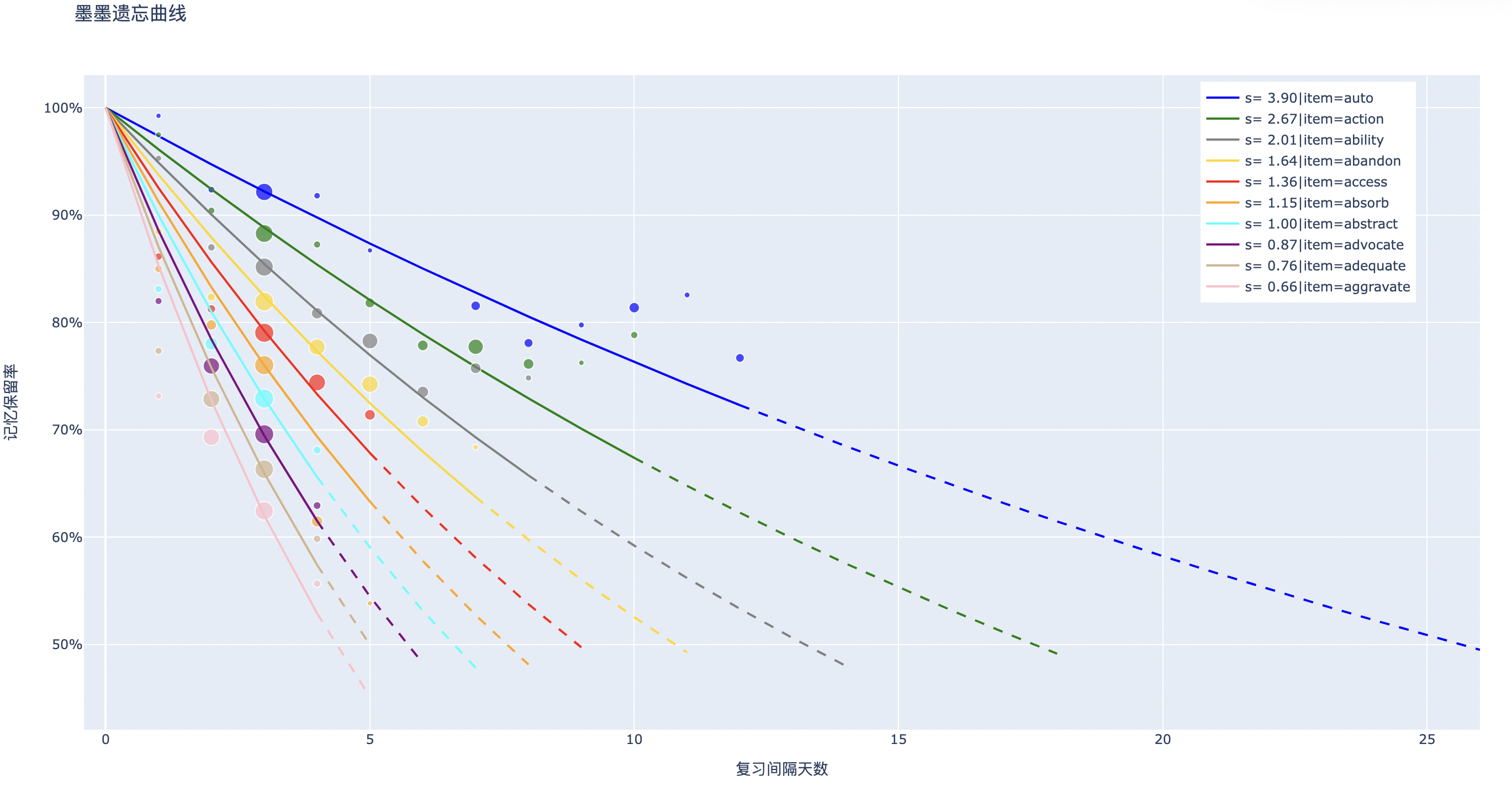
散布図の座標は$(\Delta t_i , p_i)$で、相対サイズは$\log N$です。曲線はフィットされた忘却曲線です。
最後に、難易度に取り組む時が来ました。記憶イベントデータから難易度をどのように導き出すことができるでしょうか?簡単な思考実験から始めましょう。学習者のグループが「apple」と「accelerate」という単語を初めて覚えると仮定します。記憶イベントデータを使用して、これら2つの単語の難易度をどのように区別できるでしょうか?
最も簡単な方法は、翌日にすぐテストを行い、記憶イベントデータを記録し、どちらの単語がより高い成功率を持つかを確認することです。その後、対応する安定性の値を計算できます。
つまり、最初のレビュー後の安定性が難易度を反映することができます。しかし、難易度の推定には標準的な方法はありません。これは入門記事なので、難易度の計算問題については詳しく説明しません。想起可能性と安定性とは異なり、難易度は明確な定義を持たない曖昧な概念です。
初心者はここでストップ
この記事の残りの部分は、私の研究に関する詳細な内容を扱っています。学問に不慣れな方は、ここで止めて、これまでの3日間の内容を復習してください。以下の内容に興味がある方は、読み進めてください。
状態遷移
これまでのところ、記憶イベントデータを記憶状態に変換することができます:
$$ (item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , p_i, N) => (D_i, S_i, R_i) $$
次に、状態間の関係を説明し始めることができます。レビュー後の$\Delta t$日後の記憶状態$(D_i, S_i, R_i)$と$t$、$r$の関係は何でしょうか?想起結果が$r$で、新しい記憶状態$(D_{i+1}, S_{i+1}, R_{i+1})$を得る場合です。
まず、記憶状態データを分析に適した形式に整理する必要があります:
$$ (D_i, S_i, R_i, \Delta t, r, D_{i+1}, S_{i+1}, R_{i+1}) $$
ここで、レビュー後に$R_{i+1}$はすぐに100%に達するため、分析中に無視できます。また、$R_i$、$\Delta t$、$S_i$のうち2つを知っていれば3つ目を決定できるため、$\Delta t$も無視できます。
最終的に、分析する必要がある状態データは次のとおりです:
$$ (D_i, S_i, R_i, r, D_{i+1}, S_{i+1}) $$
そして、$\cfrac{S_{i+1}}{S_i}=SInc$は、記憶の安定性増加の章で述べたパターンを参照することができます:
$$ SInc = a S^{-b} $$
$$ SInc = c e^{-d R} $$
難易度$D$の影響はここでは省略して、関係式を得ることができます:
$$ S_{i+1} = S_{i} \cdot a S_{i}^{-b} e^{-c R_i}\textrm{(if r = 1)} $$
上記の式に従って、各成功した想起後の学習者の記憶状態$(D_{i+1}, S_{i+1})$を予測できます。忘却に対するフィードバックも同様であり、別の状態遷移方程式セットで説明できます。
間隔反復システムのシミュレーション
DSR記憶モデルを使用すると、任意のレビュー計画の下で記憶状態をシミュレートできます。では、具体的にどのようにシミュレーションすればよいのでしょうか?まず、人々が現実世界で間隔反復ソフトウェアをどのように使用するかという視点から始める必要があります。
例えば、ジャレットが4か月後にGREの準備をする必要があり、試験のために英単語を覚えるために間隔反復を使用する必要があるとします。しかし、他の科目の準備にも時間を割かなければなりません。
上記の文から、2つの明らかな制約があります:締め切りまでの日数と毎日の学習時間です。間隔反復システム(SRS)シミュレーターは、これら2つの制約を考慮する必要があります。さらに、単語の数は限られているため、SRSシミュレーションには有限のカードセットも含まれ、学習者は毎日学習とレビューのための教材を選択します。間隔反復スケジューリングアルゴリズムは、レビュータスクの配置を管理します。要約すると、SRSシミュレーションには以下が必要です:
- 教材セット
- 学習者
- スケジューラー
- シミュレーション期間(1日内 + 合計日数)
学習者はDSRモデルを使用してシミュレートでき、各レビューに対してフィードバックと記憶状態を提供します。スケジューラーは、SM-2、ライトナーシステム、または他のレビューをスケジューリングするためのアルゴリズムを使用できます。
次に、SRSシミュレーションの2つの次元に基づいて具体的なシミュレーションプロセスを設計します。明らかに、未来に向かって日ごとにシミュレーションする必要があり、各日のシミュレーションはカードからのフィードバックで構成されます。したがって、SRSシミュレーションは2つのループで構成できます:外側のループは現在のシミュレートされた日付を表し、内側のループは現在のシミュレートされたカードを表します。内側のループでは、各レビューに費やす時間を指定する必要があります。累積時間が1日の学習時間の制限を超えると、ループは自動的に終了し、次の日に進む準備が整います。
以下はSRSシミュレーションの疑似コードです:

興味のある読者のために、関連するPythonコードがGitHubでオープンソース化されています:L-M-Sherlock/space_repetition_simulators: Spaced Repetition Simulators (github.com)
SSP-MMCアルゴリズム
DSRモデルとSRSシミュレーションについて議論した後、与えられたレビュー計画の下で学習者の記憶状態と記憶状況を予測できるようになりましたが、最終的な質問にはまだ答えていません:最も効率的なレビュー計画はどのようなものでしょうか?最適なレビュー計画を見つけるにはどうすればよいでしょうか?SSP-MMCアルゴリズムは、最適制御の観点からこの問題を解決します。
SSP-MMCは、確率的最短経路(Stochastic Shortest Path)と記憶コスト最小化(Minimize Memorization Cost)の略であり、アルゴリズムの基盤となる数学的ツールキットと最適化目標の両方をカプセル化しています。以下の議論は、私の大学院論文「LSTMと間隔反復モデルに基づくレビュー計画アルゴリズムの研究」と、会議論文「間隔反復スケジューリングを最適化するための確率的最短経路アルゴリズム」から適応されています。
問題設定
間隔反復アルゴリズムの目的は、学習者が効率的に長期記憶を形成するのを助けることです。記憶の安定性が長期記憶の保持強度を測定する一方で、反復の回数と反復ごとに費やされる時間は記憶のコストを反映します。したがって、間隔反復スケジューリングの最適化の目標は、与えられた記憶コストの制約内でできるだけ多くの教材を目標の安定性に到達させるか、最小の記憶コストで一定量の記憶された教材を目標の安定性に到達させることです。その中で、後者の問題は、1つの記憶教材を最小の記憶コストで目標の安定性に到達させる方法(MMC)として簡略化できます。
DSRモデルはマルコフ性を満たします。DSRモデルでは、各記憶の状態は最後の安定性、難易度、現在のレビュー間隔、およびリコールの結果にのみ依存し、これはレビュー間隔に基づくランダムな分布に従います。安定性状態遷移のランダム性のため、教材を目標の安定性に到達させるために必要なレビューの回数は不確定です。したがって、間隔反復スケジューリングの問題は無限時間の確率的動的計画問題と見なすことができます。長期記憶を形成する場合、この問題には終了状態があり、それが目標の安定性です。したがって、これは確率的最短経路(SSP)問題です。
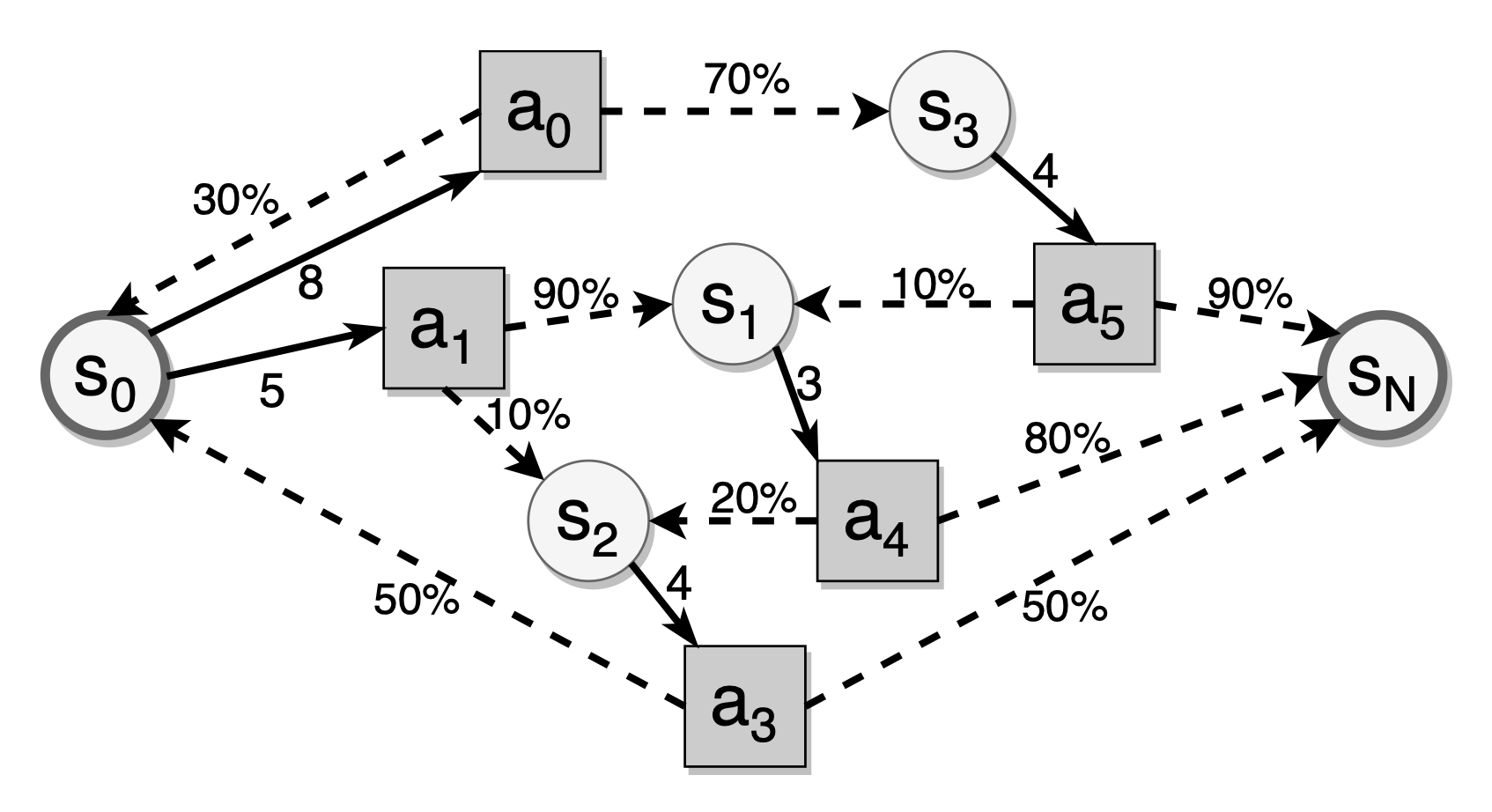
上記の図に示されているように、円は記憶状態を、四角はレビューアクション(つまり、現在のレビュー後の間隔)を表し、破線の矢印は特定のレビュー間隔に対する状態遷移を示し、黒いエッジは特定の記憶状態で利用可能なレビュー間隔を表します。間隔反復における確率的最短経路問題は、目標状態に到達するための期待されるレビューコストを最小化する最適なレビュー間隔を見つけることです。
定式化
この問題を解決するために、各フラッシュカードのレビュー過程を、状態集合$\mathcal{S}$、アクション集合$\mathcal{A}$、状態遷移確率$\mathcal{P}$、およびコスト関数$\mathcal{J}$を持つマルコフ決定過程(MDP)としてモデル化できます。アルゴリズムは、目標状態$s_N$に到達するための期待されるレビューコストを最小化する方策$\pi$を見つけることを目指します。
$$ \begin{aligned} \pi^* = \arg\min_{\pi \in \Pi} \lim_{{N \to \infty}} \mathbb{E}_{s_{0}, a_{0}, \ldots} \left[ \sum_{t=0}^{N} \mathcal{J}(s_{t}, a_{t}) \mid \pi \right] \end{aligned} $$
状態空間$S$は記憶モデルの状態サイズに依存します。DSRモデルでは、状態変数は2つしかないため、状態は$s = (D, S)$として定式化できます。アクション空間$\mathcal{A} = {\Delta t_1, \Delta t_2, \ldots, \Delta t_n }$は、スケジュール可能な$N$個の間隔で構成されます。状態遷移確率$\mathcal{P}_{s,a}(s')$は、状態$s$およびアクション$a$の下でフラッシュカードが想起される確率を表します。コスト関数$\mathcal{J}$は次のように定義されます:
$$ \begin{aligned} \mathcal{J}(s_0) &= \lim_{{N \to \infty}} \mathbb{E} \left[ \sum_{{t=0}}^{N-1} g_t(s_t, a_t(s_t), r_t) \right] \ r_t &\sim \text{Bernoulli}(p_t) \end{aligned} $$
ここで、$g_t$はステージごとのコストであり、$r_t$はベルヌーイ分布に従う想起の結果です。目標状態$s_N$は、望ましい記憶の安定性レベルに対応します。
アルゴリズム
マルコフ決定過程$\text{MDP}(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{J})$を値反復法を用いて解きます。ベルマン方程式は次の通りです:
$$ \begin{aligned} \mathcal{J}^*(s) &= \min_{a \in \mathcal{A}(s)} \left[ \sum_{s'} \mathcal{P}_{s,a}(s') \left( g(r) + \mathcal{J}^*(s') \right) \right]\ s' &= \mathcal{F}(s,a,r,p) \end{aligned} $$
ここで、$\mathcal{J}^*$は最適コスト関数を表し、$\mathcal{F}$はDSRモデルの文脈内での状態遷移関数を表します。簡単のために、想起の応答のみを考慮します:$g(r) = a \cdot r + b \cdot (1-r)$、ここで$a$は成功した想起のコスト、$b$は失敗した想起のコストです。
上記のベルマン方程式に基づいて、値反復アルゴリズムはコストマトリックスを使用して最適コストを記録し、ポリシーマトリックスを使用して反復中の各状態に対する最適なアクションを保存します。

各記憶状態に対して各オプションのレビュー間隔を連続的に反復し、現在のレビュー間隔を選択した後の期待される記憶コストをコストマトリックスの記憶コストと比較し、現在のレビュー間隔のコストが低い場合は、対応するコストマトリックスとポリシーマトリックスを更新します。最終的に、すべての記憶状態に対する最適な間隔とコストが収束します。
このようにして、最適なレビュー方策を得ることができます。記憶状態を予測するためのDSRモデルと組み合わせて、SSP-MMCアルゴリズムを使用して各学習者に最も効率的なレビュー計画を配置できます。
このアルゴリズムはMaiMemoのGitHubリポジトリでオープンソース化されています:maimemo/SSP-MMC: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling (github.com)。詳細な検討に興味のある読者は、ローカルでの探索のためにコピーをフォークすることをお勧めします。
結論
最後までお疲れ様でした!ここまで諦めずに読み進めたあなたは、すでに間隔反復アルゴリズムの世界に足を踏み入れています!
まだ多くの疑問が残っているかもしれません。その中には答えが見つかるものもあれば、まだ未開拓の領域も多くあります。
私がこれらの疑問に答える能力は非常に限られていますが、間隔反復アルゴリズムの最前線を進めるために一生を捧げる覚悟です。
記憶の謎を解き明かす旅に、ぜひ一緒に参加してください!
参考文献
間隔反復スケジューリングを最適化するための確率的最短経路アルゴリズム | 第28回ACM SIGKDD知識発見とデータマイニング会議の議事録
記憶の動態を捉えて間隔反復スケジュールを最適化する | IEEEジャーナル&マガジン | IEEE Xplore
オリジナルリンク: https://l-m-sherlock.github.io/thoughts-memo/post/srs_algorithm_introduction/